Оценочные средства
для проведения текущего контроля и промежуточной аттестации
по УД .ЕН.01 Математика
основной профессиональной образовательной программы
по специальности СПО 205405 Технология комплексной переработки древесины
Форма проведения оценочной процедуры:
экзамен
Новодвинск 2013
Разработчики:
ГАОУ СПО Архангельской области «Новодвинский индустриальный техникум», методист, преподаватель математики Г.В. Гурьева
(место работы) (занимаемая должность) (инициалы, фамилия)
I.Паспорт комплекта оценочных средств
Таблица 1
|
Предмет(ы) оценивания
(1)
|
Объект(ы) оценивания
(2)
|
Показатели
оценки
(6)
|
|
|
|
|
|
Уметь:
|
|
|
|
составлять уравнения прямых по заданным условиям и изображать их на координатной плоскости;
|
Составление
уравнений прямых на плоскости по заданным условиям и изображение их на координатной плоскости;
|
Составление уравнений прямых:
с угловым коэффициентом; общего уравнения; проходящей через две точки; проходящей через данную точку в данном направлении и их изображение на координатной плоскости.
Вычисление угла между двумя прямыми, условие параллельности и перпендикулярности прямых. Вычисление расстояния от точки до прямой.
|
|
вычислять пределы функций с помощью раскрытия неопределённостей и формул первого и второго замечательных пределов;
|
Вычисление
пределов функций с применением теорем о пределах, приёмов раскрытия неопределённостей.
|
Вычисление
пределов функций в точке и при х→∞ с применением теорем о пределах, приёмов раскрытия неопределённостей и формул первого и второго замечательных пределов;
|
|
находить производные и дифференциалы сложных функций, исследовать функции и строить графики с помощью производных;
|
Нахождение производных и дифференциалов сложных функций, исследование функций и построение графиков с помощью производных. Применение производной к решению прикладных задач.
|
Нахождение производных и дифференциалов элементарных и сложных функций.
Исследование функций на выпуклость, вогнутость и перегиб.
Исследование функций, имеющих точки разрыва, и построение их графиков с помощью производных. Решение задач прикладного характера при помощи дифференциального исчисления.
|
|
находить неопределённые и определённые интегралы основными методами, применять геометрические и физические приложения определённого интеграла;
|
Нахождение
неопределённых и определённых интегралов основными методами, применение интеграла к решению прикладных задач в области профессиональной деятельности.
|
Вычисление неопределённых интегралов методом замены переменной, методом интегрирования по частям, интегрирование простейших рациональных и иррациональных функций.
Вычисление определённых интегралов основными методами.
Применение определённого интеграла для вычисления площадей плоских фигур, объёмов тел вращения; Механические приложения определённого интеграла, задачи практического производственного содержания по данной теме, составленные обучающимися.
|
|
решать дифференциальные уравнения первого порядка с разделяющимися переменными, линейные и однородные дифференциальные уравнения
|
Методы решения дифференциальных уравнений первого порядка.
|
Решение дифференциальных уравнений первого порядка: с разделяющимися переменными (общее и частное решения),однородных, линейных (метод И.Бернулли)
|
|
вычислять вероятности случайных событий, числовые характеристики дискретной случайной величины;
|
Способы
вычисления вероятностей случайных событий, числовых характеристик дискретной случайной величины.
|
Нахождение вероятностей, применяя классическое определение, формулы комбинаторики и основные теоремы вероятностей.
Построение многоугольника распределения по заданному закону распределения дискретной случайной величины.
Решение задач на нахождение математического ожидания, дисперсии и среднего квадратического отклонения по заданному закону распределения.
|
|
задавать выборочные распределения, вычислять выборочные характеристики.
|
Выборочный метод в математической статистике.
|
Построение статистического распределения по заданным значениям выборки, построение полигона частот, нахождение эмпирической функции по данному распределению выборки.Вычисление выборочной средней и выборочной дисперсии, если заданы интервалы результатов измерений плотности древесины.
|
|
Знать:
|
|
|
|
виды уравнений прямой на плоскости, условия параллельности и перпендикулярности прямых;
|
Основные понятия аналитической геометрии на плоскости.
|
Формулы уравнений прямых: с угловым коэффициентом; общего уравнения; проходящей через две точки; проходящей через данную точку в данном направлении Формулы для вычисления угла между двумя прямыми, условия параллельности и перпендикулярности прямых.
|
|
определение предела функции в точке и на бесконечности, теоремы о пределах, формулы двух замечательных пределов, методы раскрытия неопределённостей;
|
Основные понятия теории пределов.
|
Теоремы о пределах функций, основные методы раскрытия неопределённостей.
|
|
-определения производной и дифференциала, правила дифференцирования, общую схему построения графиков с помощью производной;
|
Основные понятия и методы дифференциального исчисления.
|
Основные понятия дифференциального исчисления: определения производной и дифференциала, правила дифференцирования, механический и геометрический смысл производной, уравнение касательной к графику функции.
Необходимые и достаточные условия возрастания и убывания функции, определения критических точек и экстремумов функции.
Правила исследования функции на экстремум, точки перегиба. Определения асимптот графика функции. Правило нахождения наибольшего и наименьшего значений функции на отрезке.
|
|
определения и свойства неопределённого и определённого интегралов, способы вычисления интегралов, формулы применения определённого интеграла при вычислении площадей плоских фигур, объёмов тел вращения;
|
Основные понятия и методы интегрального исчисления.
|
Определения и свойства неопределённого и определённого интегралов, формулы интегрирования.
Методы вычисления определённых интегралов.
|
|
определение и способы решения дифференциальных уравнений первого порядка;
|
Определение и способы решения дифференциальных уравнений первого порядка.
|
Определения: дифференциального уравнения первого порядка, общего и частного решений (задача Коши). Способы решения дифференциальных уравнений первого порядка.
|
|
определение вероятности случайного события, основные формулы теории вероятностей, числовые характеристики дискретной случайной величины;
|
Основные понятия и формулы теории вероятностей.
|
Определение вероятности случайного события, основные формулы теории вероятностей, числовые характеристики дискретной случайной величины.
|
|
понятие выборки, выборочного распределения, выборочных характеристик.
|
Основные понятия и выборочные характеристики математической статистики.
|
Понятие выборки, определение эмпирической функции распределения, полигона и гистограммы частот. Определения выборочной средней и выборочной дисперсии.
|
Описание правил оформления результатов оценивания.
Оценивание производится по 5-ти балльной шкале.
Оценка практической работы обучающихся:
Отметка «5» ставится, если:
-
работа выполнена полностью, самостоятельно;
-
в логических рассуждениях и обосновании решения нет ошибок;
-
в решении нет математических ошибок (возможна одна неточность, не являющаяся следствием незнания или непонимания учебного материала)
Отметка «4» ставится, если:
Отметка «3» ставится, если:
Отметка «2» ставится, если:
-
допущены существенные ошибки, показавшие, что обучающийся не владеет обязательными умениями по этой теме
-
Оценка обучающегося при устном и письменном опросе проводится по 5-ти балльной шкале.
Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а его изложения математически грамотны и отличаются последовательностью.
Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены все вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
Общая оценка выставляется с учётом текущих оценок.
Шкала оценки образовательных достижений
|
Процент результативности (правильных ответов)
|
Оценка уровня подготовки
|
|
балл (отметка)
|
вербальный аналог
|
|
90 ÷ 100
|
5
|
отлично
|
|
80 ÷ 89
|
4
|
хорошо
|
|
60 ÷ 79
|
3
|
удовлетворительно
|
|
менее 60
|
2
|
неудовлетворительно
|
II. Комплект оценочных средств
2.1. Задания
ЗАДАНИЕ № 1.
Практическая работа № 3
Тема: Пределы функций.
Найти указанные пределы функций (не пользуясь правилом Лопиталя ). Варианты: 1-10

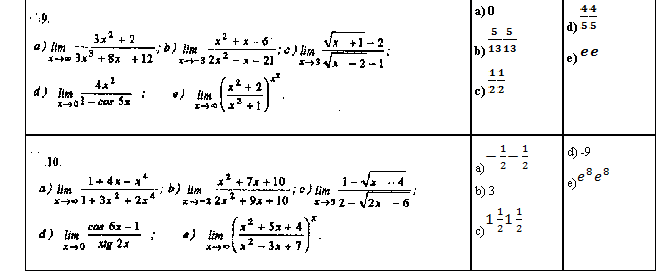
|
Предмет(ы)
Оценивания (1)
|
Объект(ы)
Оценивания (2)
|
Показатели оценки
(6)
|
Критерии оценки (7)
|
|
Вычислять пределы функций с помощью раскрытия неопределённостей и формул первого и второго замечательных пределов;-
|
Вычисление
пределов функций с применением теорем о пределах, приёмов раскрытия неопределённостей.
|
Вычисление
пределов функций в точке и при х→∞ с применением теорем о пределах, приёмов раскрытия неопределённостей и формул первого и второго замечательных пределов;-
|
Правильность применения приёмов раскрытия неопределённостей и формул первого и второго замечательных пределов.
|
|
Условия выполнения задания:
1. Место выполнения задания: учебный кабинет.
2. Максимальное время выполнения задания:45 мин.
3. Вы можете воспользоватьсясправочными материалами по данной теме
|
Критерии оценки практической работы по пятибалльной шкале:
«5» - все задания выполнены верно, самостоятельно, допускается один недочет.
«4» - все задания выполнены полностью, самостоятельно, но допущена одна ошибка.
«3» - выполнено верно три задания, самостоятельно.
«2» - выполнено верно менее трех заданий.
Задание №2.
Практическая работа №5.
Тема: Исследование функций на выпуклость, вогнутость и перегиб.
Исследовать данные кривые на выпуклость, вогнутость и перегиб. (1вариант-нечётные номера заданий, 2вариант-чётные номера заданий).


|
Предмет(ы)
оценивания
|
Объект(ы)
оценивания
|
Показатели оценки
|
Критерии оценки
|
|
Находить производные и дифференциалы сложных функций, исследовать функции и строить графики с помощью производных.
|
Исследование функций и построение графиков с помощью производных.
|
Исследование функций на выпуклость, вогнутость и перегиб.
|
Соблюдение последовательности алгоритма нахождения точек перегиба.
Правильность применения определения выпуклости графика функции, достаточного условия существования точек перегиба.
|
|
Условия выполнения задания:
1. Место выполнения задания: учебный кабинет.
2. Максимальное время выполнения задания:20 мин.
3. Вы можете воспользоватьсяформулами дифференцирования.
|
Критерии оценки практической работы по пятибалльной шкале:
«5» - все три задания выполнены верно, самостоятельно.
«4» - все три задания выполнены полностью, самостоятельно, но допущена одна ошибка.
«3» - выполнено верно два задания, самостоятельно.
«2» - выполнено верно менее двух заданий практической работы.
|









